日本応用数理学会
2019年 研究部会連合発表会
プログラム
ご注意：本プログラムは暫定版であり変更される可能性があります．
| 1月25日 |
プログラム公開 |
| 2月6日 |
プログラム更新 |
3月4日
3月5日
▷ 行列・固有値問題の解法とその応用（１） ［3月4日：09:40-11:00：A］
- 分子モータの集団的運動を解析する３次元超疎視化分子動力学コードでの準陰解法の効用について / ○鷲尾 巧 (UT-Heart研究所/東京大学), 久田 俊明 (UT-Heart研究所/東京大学) [概要]
我々はミオシン-アクチン間の架橋運動が引き起こすサルコメアの収縮および伸長運動を解析するための超疎視化３次元分子動力学コードを開発した. 超疎視化の利点は粘性係数の増加および剛性係数の緩和の相乗効果により従来の分子動力学コードに比べ大きな時間ステップ(1fs→50ps)が適用でき, １ステップあたりの計算量も削減できるところにある. しかしながらこれでも心臓の１拍動にあたる１秒の計算に１週間以上を要している. ここでは, 時間ステップを制約している強い剛性を伴う相互作用のみを選択し, LU分解の負荷を小さくした準陰解法を適用することによりさらなる高速化を図る試みについて報告する.
- ◎一般化エルミート固有値問題の部分固有値計算における周回積分に基づく精度保証法の改良 / 今倉 暁 (筑波大学), ○保國 惠一 (筑波大学), 高安 亮紀 (筑波大学) [概要]
一般化エルミート固有値問題における指定領域内全ての固有値（部分固有値）を精度保証することを考える。これまで提案してきた周回積分に基づく部分固有値の精度保証法を改良し、各積分点に関する線形方程式の数値解を精度保証する手間を省く手法を提案する。数値実験により、提案法が計算効率に関して従来法に匹敵し、特に疎行列に対して有効であることを示す。
- 非線形固有値問題へのBlock Arnoldi法の適用とその収束性について / ○長坂 英明 (慶應義塾大学理工学研究科基礎理工学専攻), 野寺 隆 (慶應義塾大学理工学部) [概要]
本発表では非線形固有値問題の近似解法について考える．このような問題は流体力学などで現れることが多い．問題の近似解法には，近年，解法の安定性が比較的高い反復法が用いられ，Arnoldi法を発展させたInfinite Arnoldi法が有効な解法である．そこで，我々はこの手法をブロック化した，Block infinite Arnoldi法を提案し，数値実験を通して従来法と比較検討を行い，提案手法の有効性を示す．
- ◎リーマン多様体上の最適化におけるレトラクションの理論と応用 / ○佐藤 寛之 (京都大学), 相原 研輔 (東京都市大学) [概要]
本発表では，リーマン多様体上の最適化において，任意の多様体上で与えられたレトラクションをもとに，同相な多様体上の新たなレトラクションを構成するための理論を示す．また，具体的に，シュティーフェル多様体上のレトラクションから一般化シュティーフェル多様体上のレトラクションを構成し，その効率的な実装についても議論する．さらに，一般化シュティーフェル多様体上の最適化の応用として，正準相関分析に関連する数値例を紹介する．
▷ 行列・固有値問題の解法とその応用（２） ［3月4日：11:10-12:30：A］
- ◎逆一般化固有値問題に対する二次収束解法とその収束理論 / ○相島 健助 (法政大学) [概要]
逆固有値問題とは，指定した固有値とある種の構造を有する行列を構成することを目的とする逆問題である．古典的には，Sturm-Liouville 問題の逆問題の定式化としてよく利用されていたが，近年，諸問題への応用が検討されその数値解法は重要視されている．本発表では，逆一般化固有値問題において特に重複固有値を指定する場合に焦点を当て，新たな二次収束解法を与え，その数値例と収束理論を報告する．
- フィルタの反復による固有値問題の近似対の改良 / ○村上 弘 (首都大学東京) [概要]
実対称定値一般固有値問題の固有対で指定区間に固有値があるものをフィルタを用いて解く．フィルタはレゾルベントを用いて構成する．レゾルベントの作用を実現する連立１次方程式は直接法で解くものとする．単一のレゾルベントの多項式をフィルタに採用すれば行列分解に掛かるコストは最小にできるが，実現できる伝達特性はあまり良くないので近似対の残差もあまり小さくならない．しかし直交化と併せたフィルタの適用を数回反復して改良すれば，残差の小さい近似対が得られる．
- ◎ 対称行列の近似固有ベクトルと一般行列特異ベクトルのシャープな誤差評価 / ○中務 佑治 (国立情報学研究所) [概要]
対称行列の近似固有ベクトルの誤差評価にはDavis-Kahanの古典的結果が広く使われる．しかし，射影法（Rayleigh-Ritz法）を用いて抽出された近似固有ベクトルの誤差はDavis-Kahanで評価すると過剰な過大評価になることが多い．本研究ではRayleigh-Ritz法で得られた固有ベクトルに対し（使う情報を用いて改良できないという意味で）シャープな誤差評価を与える．多くの場合Davis-Kahanを大きく改善することができる．同様の結果を射影法で計算される特異ベクトルに対しても導出する．
- ◎選択的中間固有対計算と有機デバイス材料への応用 / ○星 健夫 (鳥取大), 李 東珍 (名古屋大), 桑田 亨成 (鳥取大), 角田 皓亮 (鳥取大), 曽我部 知広 (名古屋大), 張 紹良 (名古屋大) [概要]
番目を指定した選択的中間固有対計算(k-th eigenvalue problem, k-ep)手法とソルバーコードの発展，および，大規模(100万次元以上)疎行列問題への応用を報告する．産業問題として，フレキシブル（紙のように柔らかい）デバイスの基盤材料である，有機半導体薄膜を取りあげた．デバイス性能は，乱れのある系における特定（最高占有準位付近）固有対の寄与が支配的であるため，当該固有対だけを選択的に計算する需要が生じる．
▷ 行列・固有値問題の解法とその応用（３） ［3月4日：13:30-14:50：A］
- 【招待講演】Generalized Krylov subspace methods for l_p-l_q minimization with application to image restoration / ○Reichel Lothar (Kent State University), Buccini Alessandro (Kent State University), Huang Guangxin (Chengdu University of Technology), Lanza Alessandro (University of Bologna), Morigi Serena (University of Bologna), Sgallari Fiorella (University of Bologna) [概要]
This talk presents new efficient approaches for the solution of l_p-l_q minimization problems based on the application of successive orthogonal projections onto generalized Krylov subspaces of increasing dimension. The subspaces are generated according to the iteratively reweighted least-squares strategy for the approximation of
l_p- and l_q-norms or quasi-norms by using weighted l_2-norms. Computed image restoration examples illustrate the performance of the methods discussed.
- ◎積型Bi-CG法における包括的な安定化多項式の提案 / ○相原 研輔 (東京都市大学) [概要]
積型Bi-CG法は，安定化多項式の違いによりCGS法，Bi-CGSTAB法，Bi-CGStab2法，Bi-CGstab(L)法，GPBi-CG法などがあるが，これらを包含する新しい安定化多項式を提案する．提案する多項式はL+1個のパラメータを持ち，その選択によっていずれの解法へも帰着できる．また，残差を局所的に最小化するようにパラメータを決定する方法をGPBi-CGstab(L)法と名付け，その有効性を数値実験により示す．
- 行列のグレースケール画像を用いたBiCG法の収束予測の試み / ○太田 凌 (筑波大学大学院図書館情報メディア研究科), 長谷川 秀彦 (筑波大学図書館情報メディア系) [概要]
本研究ではSuiteSparse Matrix Collectionの非対称疎行列875個を係数とする連立一次方程式に対してBiCG法の収束予測を試みた. 非零要素パターンと値から256階調のグレースケール画像を生成し, BiCG法の収束予測をする二値分類器を作成した. 画像のサイズを変え, 評価には5-fold交差検証を行い, 収束する行列234個, 収束しない行列234個を用いて学習とテストを行った. その結果, 倍精度演算で前処理無しの場合に112×112(pixel)の時, 約76%の正答率で収束を予測できた.
▷ 行列・固有値問題の解法とその応用（４） ［3月4日：15:00-16:20：A］
- ◎行列余弦関数に対する数値的検証法 / ○佐藤 大 (岩手大学), 宮島 信也 (岩手大学) [概要]
行列余弦関数の値を含む区間を数値計算により求める方法を提案する. この方法は数値計算による固有分解に基づくものであり, いくつかの仮定下で行列の次元の３乗に比例する演算回数で実行可能である. 数値例により, この方法の有効性を示す.
- ◎Computing intervals containing Moore-Penrose inverses / ○Miyajima Shinya (Iwate University) [概要]
An algorithm is proposed for computing intervals containing the Moore-Penrose inverses. This algorithm is based on the Ben-Israel iteration. We particularly emphasize that the algorithm is applicable even for rank deficient matrices.
- Inverse scaling and squaring の改善による行列対数関数の高精度計算法 / ○中村 真輔 (秋田県立大学) [概要]
スカラの関数と同様の定義により得られる行列関数のひとつとして行列対数関数があり，機械学習への応用が期待されている．その計算法のひとつとして行列平方根のための Newton 法と有理関数近似を組み合わせた inverse scaling and squaring が知られている．ただしこの計算法では Newton 法から有理関数近似へ移る際に大きな桁落ちが発生する場合があるため，その改善手順について提案する．
- ◎二重指数関数型公式を用いた行列対数関数の計算について / ○立岡 文理 (名古屋大学), 曽我部 知広 (名古屋大学), 宮武 勇登 (大阪大学), 張 紹良 (名古屋大学) [概要]
本講演では数値積分による行列対数関数の計算を考える．従来はGauss-Legendre求積を用いて計算されてきたが，入力行列が悪条件なときは被積分関数が端点で急激に変化し収束性が悪化しうる．そこで本講演では，端点特異性を持つ被積分関数にも有効な二重指数関数型（DE）公式に着目し，誤差解析に基づいた適切な積分区間の与え方を示した上で，DE公式の有用性を数値的に検証する．
▷ 応用カオス【乱数生成と評価】 ［3月4日：09:40-11:00：B］
- 乱数生成器を評価するという視点での統計的評価について / ○奥富 秀俊 (東芝情報システム) [概要]
発表者は，NIST SP.800-22等の今日利用されている乱数検定スイートは，系列のランダム性の評価が中心であって，乱数生成器を積極的に評価するという視点のものではない，という考えに至っている．本発表では生成器の評価という視点での統計的評価の一例について述べる．
- Arnold の猫写像におけるパラメーター推定の困難さの分類と乱数性向上の試み / 小森 雅弘 (福岡工業大学), ○柿本 侑毅 (福岡工業大学), 伴内 湧生 (福岡工業大学), 田村 健太郎 (福岡工業大学), 山口 明宏 (福岡工業大学) [概要]
代表的なカオス写像の一つとしてArnoldの猫写像が知られており，擬似乱数生成器に応用されている．本研究では, Arnoldの猫写像のデータ系列からパラメータを推定する問題について, 秘匿するパラメータの組み合わせによるパラメータ推定の困難さの分類を行う．結果として特定の組み合わせでは, パラメータ推定問題が一次合同方程式に帰着でき秘匿するパラメータのビット長に比例する時間でパラメータを推定できることを示す．また，Arnoldの猫写像の結合系を用いることで乱数性を向上させる試みについても報告する．
- ◎複数のNon-overlapping Template Matching検定におけるp値の結合分布の理論的評価 / ○岩崎 淳 (福岡工業大学) [概要]
NIST乱数検定ツールに含まれるNon-overlapping Template Mathching検定(NTM検定)はテンプレートの選択に自由度があり、NISTから提供されているサンプルプログラムでは188項目中148項目を占める。よって、テストセットとしての有意水準を求めるにあたり、NTM検定の検定項目間の非独立性を理解しなければならない。
NTM検定の健全性は拡張された中心極限定理に基づく。本発表では、同定理を多次元に適用し、任意の2つのテンプレートに対するNTM検定のp値の結合分布を導出する。
- ◎多層ニューラルネットワークによる乱数検定法に関する研究 / ○田邉 舟 (京都大学大学院情報学研究科), 岩崎 淳 (福岡工業大学), 梅野 健 (京都大学大学院情報学研究科) [概要]
本研究では, NIST SP 800-22では想定されていない未知の偏りを検出することを目的とし, 多層ニューラルネットワークを用いた乱数検定法のモデルを確立し, 実際にいくつかの擬似乱数に対して検定を行うことで, 本手法の検出力を確認した. また, NIST SP 800-22では検出されていない乱数に対して検定を実行し, 本手法の有用性を検討した.
▷ 応用カオス（１） ［3月4日：11:10-12:30：B］
- ◎カオス性とベイズ逆確率のエントロピーとの間の一般的な関係について: Part II / ○梅野 健 (京都大学大学院情報学研究科) [概要]
カオス性Λとベイズ逆確率のエントロピーHとの関係(H=Λ+D,D≧0)の発見について2018年9月の年会で発表したが、本講演は、
その関係性が多次元にも容易に拡張でき、ある種の(出力データYが得られた時初期値Xを推測する時の曖昧さを表す)情報量Hとカオス性
との関係性が一般性をもつことを示す。この結果は、カオス性を示す尺度であるカオス尺度とは何かを考える上で有益である。
- ◎カオス尺度とリアプノフ指数の差の解釈に基づく修正カオス尺度の提案 / ○真尾 朋行 (京都大学大学院情報学研究科/東芝情報システム株式会社), 奥富 秀俊 (東芝情報システム株式会社), 梅野 健 (京都大学大学院情報学研究科) [概要]
生体データ等の分析において，データのカオス性に着目した分析法としてカオス尺度を用いることを検討している．カオス尺度は，カオスを定量化する指標として提案されているが，リアプノフ指数と差があることが報告されている．本発表では両者の差について解釈するとともに，その差分を修正したカオス尺度について提案する．
- 変形カオス尺度によるリアプノフ指数のアルゴリズミックな推定法 / ○奥富 秀俊 (東芝情報システム) [概要]
本発表では，カオス尺度の定義を変形した変形カオス尺度を定義し，データからアルゴリズミックにリアプノフ指数を推定する手法について述べる．当手法を用いた実験結果を提示し，特にデータ量と精度に関する視点での評価と課題について考察する．
- ◎カオス判定力の向上のためのカオス尺度の改良 / ○井上 啓 (山陽小野田市立山口東京理科大学) [概要]
カオス尺度は情報理論の観点から導入されたカオスを定量化する指標であり、力学系に関する情報が時系列しか得られない場合でも計算可能といった利点がある。しかし、計算の簡略化のために入出力系の分割を等分割に固定した結果、入出力系における分割の切れ目のずれ、入出力系における直交系の違い、の影響を受け、カオス尺度が余計に高い値を取ってしまう。そこで、本発表では、これらの点を考慮したカオス尺度の改良を試みる。
▷ 応用カオス（２） ［3月4日：13:30-14:50：B］
- ◎レーザーカオスにおけるモードの同時性 / ○桒島 史欣 (福井工業大学), Mona Jarrahi (ＵＣＬＡ), Semih Cakmakyapan (ＵＣＬＡ), ⽩尾 拓也 (福井工業大学), 岩尾 憲幸 (福井工業大学), ⾕ 正彦 (福井大遠⾚セ), 栗原 ⼀嘉 (福井⼤教育), 森川 治 (海保⼤), 北原 英明 (福井大遠⾚セ), 和田 健司 (大阪府立大), 中嶋 誠 (阪⼤レーザー研) [概要]
これまで、レーザーのモードが同時に発生しているかを知る方法はなかったが、レーザーの縦モード間の光ビートと他の局部発信機としてのTHz波との差周波を取ることにより、中間周波数でレーザーカオスにおけるモードの同時発生の安定性を観測したので報告する。
- ◎古典直交多項式を用いた混合性を持つ時 系列の構成とそのカオス性 / 梅野 健 (京都大学情報学研究科数理工学専攻), ○杉本 哲 (京都大学工学部情報学科) [概要]
Chebyshev多項式はモンテカルロ法においてよく用いられている直交関数系であり、その背後にはChebyshev多項式の混合性といった性質がある。しかし、ほかの直交関数系に対して同様の取り組みがなされている例はないので、今回の発表でLegendre多項式などの物理でよく用いられる直交関数系における混合性やカオス性について述べる。
- 株価対数収益率の重ね合わせと予測について / ○大掛 雄太 (京都大学情報学研究科), 梅野 健 (京都大学情報学研究科) [概要]
金融市場の価格変動の分布は，1900 年にL.Bachelierが正規分布であるという研究を発表して以降，様々な説がある(例えば，B.MandelbrotやR.MantegnaとH.Stanleyは安定分布であるという研究を発表している).しかし、どの説も正確であるとは言い難かったり，理論的になぜその分布になるのかを説明できない.本研究では，新たな株価の分布の重ね合わせ方とその分布を提案し，それを使った株価予測を試みる.
- ◎安定分布を考慮した現代ポートフォリオ理論の拡張 / ○林 豊 (京都大学工学部情報学科), 梅野 健 (京都大学大学院情報学研究科) [概要]
ポートフォリオ選択理論は古くから研究されているが,最も有名なものは1952年にHarry Markowitzによって提唱され,現在ではModern Portfolio Theory(MPT)と呼ばれているものである.
この理論においては分散共分散法が用いられており,その明快さから現在でも幅広く利用されている.
MPTでは収益率の平均をリターン・標準偏差をリスクと定義し,それらの関係性を考える.これは収益率分布が正規分布に従っていると仮定している.
これに対してBenoit Mandelbrotは1963年に金融市場の収益率は正規分布よりも裾が太い安定分布に従うという発見を報告した.
本研究では収益率を安定分布と仮定して既存のポートフォリオ理論の拡張を試みた.
▷ 応用カオス（３） ［3月4日：15:00-16:20：B］
- ◎SGB変換とその拡張について / ○大久保 健一 (京大情報), 梅野 健 (京大情報) [概要]
安定状態から不安定状態へ系が変化する様子に関する研究は多くの興味を引きつけてきた.
系の不安定状態(カオス状態)を特徴づける量としてLyapunov指数が用いられてきた. この指数が正の場合,
カオスが発生しているとする. 講演者はLyapunov指数が0から正へ変化する際の臨界指数をSGB変換において
導出した. さらに本講演ではSGB変換を拡張した写像についても解析結果を発表する.
- ◎一般の多重積分に関するカオスモンテカルロ計算法のSuperefficiency性について / ○滝川 純一郎 (京都大学情報学研究科), 梅野 健 (京都大学情報学研究科) [概要]
本研究では，被積分関数を変換することで積分値を変えず近似的にSuperefficiency性を持たせるアルゴリズムを開発し，このアルゴリズムを用いてカオスモンテカルロ計算法を行った．また，被積分関数が実際にSuperefficiency性を持つ場合との収束速度の比較を行った．その結果，従来のカオスモンテカルロ計算法では被積分関数がSuperefficiency性を持つ必要があったため，積分領域が限られたものになってしまっていたが，より一般的な被積分関数に対しても変換を施すことで，Superefficiency性を持つ関数同様に計算の高速化が可能であることが確認された．
- ◎カオスモンテカルロ計算法の最適化 / ○XIAO JIN (京都大学工学部情報学科), 梅野 健 (京都大学大学院情報学研究科) [概要]
カオスモンテカルロ法で積分を計算する際に、被積分関数が Superefficiency 条件(SEC)を満たしていれば、計算の平均二乗誤差 (MSE) が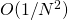 
で0に近づくSuperefficiencyが得られる。元々SECを満たさない被積分関数に対しても、Superefficiencyを得るために、その関数に前処理を行う必要がある。総サンプリング数を固定した上で前処理のための計算と本計算のサンプリング数を変えて、カオスモンテカルロ法と通常のモンテカルロ法の計算結果を比較する。
- ◎量子乱数生成の観点からみた量子コンピュータの現状 / ○田村 賢太郎 (慶應義塾大学), 鹿野 豊 (慶應義塾大学・チャップマン大学) [概要]
従来の計算機では、擬似乱数しか生成できない。これは、従来の計算機が古典物理学に基づくためである。古典物理学では初期条件によって未来が確定するため、真の乱数は生成できない。真の乱数を生成するためには、量子力学的現象を用いる必要がある。そこで、様々な量子力学的現象をソースとした量子乱数生成器の研究がなされてきた。本研究では、近年、研究開発が盛んになされている超伝導型量子コンピュータの一つであるＩＢＭ ２０量子ビットマシンを用いて一様乱数生成を試みた。その結果を紹介する。
▷ 数理政治学 ［3月4日：16:30-17:50：B］
- A generalized parametric divisor method for political apportionment / ○大山 達雄 (政策研究大学院大学), Hall Nicholas G. (The Ohio State University), 小林 和博 (東京理科大学) [概要]
議席配分問題は、可能な限り公正かつ公平な配分方法を探求すべく、200年以上も多くの研究者によって挑戦がなされている“未解決”の問題である。
筆者らによって提起された一般化パラメトリック法に基づいた、現実の各国のデータを用いた数値結果を紹介する。各国の選挙区別人口が与えられた場合に最も公正かつ公平な議席配分方法としての“不偏的な”配分方法がいかなるものか、実証分析に基づく配分方法を提起する。
- 空間を導入したVarianタイプのモデルにおいてInformed agentの分布が均衡方程式に与える影響 / 河合 信之輔 (静岡大学), ○中川 訓範 (静岡大学) [概要]
本研究では、Nakagawa (2017)で提案した空間を導入したVarianタイプのモデルにおいて、Informedな主体の分布が均衡を記述する微分方程式にもたらす影響について分析する。具体的には、従来のモデルにおいて線分上の一点にマスで分布していたInformedな主体が線分上に一様に分布する状況に拡張したモデルを考え、部分ゲームの均衡を記述する方程式がどのように変化するかを考察した。
- 取り分と配分議席数の最大乖離について / ○一森 哲男 (大阪工業大学) [概要]
アメリカの議席配分問題を扱う．州の取り分は，その州に与えられる議席の理想値とされるが，現実に配分される議席数は取り分より1議席以上の差異が生じることが知られている．この講演では，その差異はどの程度の大きさにまでなるのかを議論する．
▷ 応用可積分系（１） ［3月4日：09:40-11:00：C］
- ◎max-plus代数によるライフゲームの連続化 / ○坂田 幸太郎 (早稲田大学大学院 基幹理工学研究科), 高橋 大輔 (早稲田大学大学院 基幹理工学研究科) [概要]
2次元セルオートマトンで最も有名であろうライフゲーム(Conway’s Game of Life)について, max-plus代数を用いて時間発展方程式を定義し, 多値, 連続値への拡張を行った. さらにはセルの近傍を拡大して時間発展を行うことで, より滑らかで流動的な様相を確認することができたので紹介する.
- ◎一定周期のMax-Plus写像について / ○小俣 亮 (早稲田大学大学院基幹理工学研究科), 高橋 大輔 (早稲田大学大学院基幹理工学研究科) [概要]
本講演では，Max-Plus演算を用いた一定周期の写像に焦点を当てる．このような写像は，同じくMax-Plus演算を用いて線形な回転写像に変換することが可能であり，解も明示的に示すことができる．どのような形式のMax-Plus写像がこのような線形化可能な写像になるか，また，線形化するための変換や解の構造はどのようなものかなどについて，具体例を挙げながら紹介する．
- ◎円分多項式の積に付随する離散力学系の可積分判定について / 時弘 哲治 (東京大学大学院数理科学研究科), ○神谷 亮 (東京大学大学院数理科学研究科) [概要]
与えられたn次多項式に対し、それに付随する乗法的なｎ階の差分方程式を考える。そのような差分方程式のうち、円分多項式の積に付随するもののみ、代数的エントロピーは０（可積分）である。本研究では、円分多項式の積に付随する差分方程式に、ある種の摂動を加えたとき、可積分性が保存するための多項式及び摂動の加え方に関する条件を調べた。講演では、4階までのすべての場合の調査結果や、付随する超離散系との関係を述べる。
- ◎クラスター代数とカオス / ○野邊 厚 (千葉大学教育学部) [概要]
ランク２のクラスター代数のミューテーションから導かれる２階差分方程式の１パラメータ族について考察する。この差分方程式はパラメータの値が４以下の場合可積分であるが、パラメータの値が５以上の場合代数的エントロピーが正の値をとること、すなわちカオス系であることを示す。
▷ 応用可積分系（２） ［3月4日：11:10-12:30：C］
- リュービルの定理と保存則 / ○佐々 成正 (原子力機構) [概要]
これまで我々は、ハミルトン系における
ポアンカレ不変量(2次)と系の運動量保存則
やシンプレクティック数値積分法との関連
性について論じてきた。これを２次以上の
ポアンカレ不変量にも拡張して考察を行い
たい。
- BKP方程式のGram型Pfaffian解とそのソリトン相互作用 / ○田中 悠太 (早稲田大学), 丸野 健一 (早稲田大学), 児玉 裕治 (オハイオ州立大学) [概要]
KP II方程式はWronskian表示のソリトン解を持ち，ある条件のもとで係数行列を分類することでソリトン相互作用が分類されている．一方，BKP方程式のソリトン解はGram型Pfaffianで表されるが，その解が発散する点を持たないための条件が分かっていないため，ソリトン相互作用の分類がなされていない．本講演ではBKP方程式のソリトン解のGram型Pfaffian表示の正値性について議論する．
- 局所相互作用する自己駆動粒子系における集団運動の形成 / ○武田 龍之介 (宇都宮大学工学部), 上村 佳嗣 (宇都宮大学工学研究科), 小池 正史 (宇都宮大学工学研究科), 矢嶋 徹 (宇都宮大学工学研究科) [概要]
運動個体の多体系が秩序だった集団運動を示すことがある：微生物から鳥に至るまで普遍的に見られる．特徴は，各個体の運動が局所的に決まる場合でも集団運動が自発的に発生することである．その条件を探るため，局所相互作用下で運動する粒子系を計算機実験で追跡した．各粒子の運動方向を次の3要素で変化させる：現在の運動方向，近傍粒子の重心座標，ノイズ．これら3要素の重みを変え，集団運動が発生する条件を探索した．
- ◎確率セルオートマトンの定常分布とその極限について / ○延東 和茂 (早稲田大学) [概要]
パラレルにアップデートされるTASEPと等価なモデルである確率バーガーズセルオートマトンに対して，遷移確率行列と組み合わせ論の手法を用いて定常分布を予想し，極限計算を行いながら運動量の期待値としての基本図を導出する．また，これらの手法で定常分布と基本図が予想できる拡張系について紹介する．具体的には，上記の系の一種の多成分拡張系の漸近挙動が，高次保存量を持つ確率セルオートマトンのそれと等価であることを示す．
▷ 応用可積分系（３） ［3月4日：13:30-14:50：C］
- A hinged linkage mechanism that follows discrete integrable equations / ○Park Hyeongki (Graduate School of Mathematics, Kyushu University), Kaji Shizuo (Institute of Mathematics for Industry, Kyushu University), Kajiwara Kenji (Institute of Mathematics for Industry, Kyushu University) [概要]
We consider a family of linkage mechanisms which consist n-copies of a rigid body joined together by hinges to form a ring. Each hinge joint has its own axis of revolution and rigid bodies joined to it can be freely rotated around the axis. The family includes a special family of linkages called the Kaleidocycles which exhibit a “turning over” motion. We can represent the Kaleidocycles as discrete closed space curves with a constant torsion up to sign, where Kaleidocycle motion preserves arc length at each pair of curve points. We present particular paths in the configuration space of the Kaleidocycles, which are governed by the semi-discrete mKdV and sine-Gordon equations.
- 相似可積分幾何を用いた対数型美的曲線の空間曲線への拡張 II / 井ノ口 順一 (筑波大), ○梶原 健司 (九大IMI), 三浦 憲二郎 (静岡大), Schief Wolfgang K. (University of New South Wales) [概要]
工業意匠設計において提唱された，美的特性をもつ平面曲線である対数型美的曲線（LAC）の相似幾何による定式化を拡張し，LACの空間曲線への拡張を提案する．提案する曲線は，相似幾何における弧長係数表示された空間曲線の可積分変形を記述する方程式の進行波解で特徴付けられ，相似捩率がヤコビの楕円函数，相似曲率はLamé函数で記述される．また，捩率を0にする極限でLACに帰着する．
- ◎Lanczos-Phillips アルゴリズムの連分数計算への応用とその直交多項式に基づく拡張について / ○澤 薫 (京都大学), 中村 佳正 (京都大学) [概要]
Lanczos-PhillipsアルゴリズムはHankel行列の修正Cholesky分解を計算する手法の一つで，Hankel行列式の満たす関係式として，実軸上の直交多項式の3項漸化式から導出することができる．本講演では，Laurent双直交多項式からToeplitz行列のLU分解を計算するアルゴリズムが導出できることを示すとともに，連分数計算のFGアルゴリズムに比べて除算の回数が少なく、高速に連分数を計算できることを示す．
- ◎ある帯行列の逆固有値問題の解法について / ○赤岩 香苗 (京都産業大学), 前田 一貴 (関西学院大学) [概要]
指定した固有値をもつ行列を構成する問題を逆固有値問題という。本講演では、「ギザギザ」の5重対角行列の逆固有値問題に対して、直交ローラン多項式を用いた解法を提案する。
▷ 計算の品質（１） ［3月4日：15:00-16:20：C］
- 非線形関数微分方程式の周期解の精度保証付き数値解法 / ○大石 進一 (早稲田大学理工学術院応用数理学科) [概要]
多くの非線形遅延微分方程式の周期解が
S.Oishi: Numerical Verification of Existence and Inclusion of Solutions for Nonlinear Operator Equations, J. Computational and Applied Math., 60, pp.171-185 (1995)
の方法（の変形）によって統一的に求められることを示す。数理的にはNewton-Kantorovich型定理の変形、線形化作用素の逆作用素ノルムの評価法など適用にあたり様々な数理的に興味ある問題が生じることを述べ、その解決策を論じる。精度保証例を述べ、新しく発見した現象についても言及する。
- Poisson方程式に対する構成的高次誤差評価 / ○渡部 善隆 (九州大学), 木下 武彦, 山本 野人 (電気通信大学), 中尾 充宏 (早稲田大学) [概要]
2次元Poisson方程式の有限要素近似に対する誤差評価定数を構成的に求める方法について考察します．方程式の右辺に特別な条件を課した時に高次の収束オーダーを持つ事前誤差評価が得られることを理論的に示すとともに，先行研究である事後誤差評価と比較することでその有効性と応用を議論します．
- 微分作用素の固有ベクトルの厳密評価について / ○劉 雪峰 (新潟大学), Vejchodsky Tomas (Czech Academy of Sciences) [概要]
これまでの数年間の研究では、有限要素法を利用することで、効率的な微分作用素の厳密な固有値評価方法（上界と下界の評価を与えること）がすでに提案されている。本研究では、微分作用の固有値評価の厳密評価を用いて、固有値ベクトルの厳密な評価方法を初めて提案する。特に、固有値が属する固有空間の次元が１以上となる場合、近似固有ベクトル空間と実際の固有空間の間の距離への厳密な評価が可能である。
- ◎時間発展方程式の線形化問題に対する解作用素の厳密評価 / ○高安 亮紀 (筑波大学) [概要]
時間発展方程式に対する解の精度保証付き数値計算を考える際に、数値計算で得られた近似解における線形化問題の解作用素を考える場合がある。これはある斉次線形偏微分方程式の初期値問題となり、本講演ではこの偏微分方程式の解の評価を得る計算機援用手法を紹介する。より具体的には、フーリエ級数によって離散化した常微分方程式系の基本解の評価と、無限次元部分の発展作用素の評価を組み合わせ、解作用素の評価を得る。
▷ 計算の品質（２） ［3月4日：16:30-17:50：C］
- 第二種ベッセル関数の精度保証付き数値計算法 / ○工藤 直輝 (早稲田大学), 柏木 雅英 (早稲田大学) [概要]
ベッセルの微分方程式は弾性波動や円筒内での熱伝導を表す際に用いられ、その特殊解は、第一種ベッセル関数と、第二種ベッセル関数の和で表すことが出来る。整数次のベッセル関数はすでに精度保証する手法が提案されているが、非整数次のベッセル関数は未だされていない。今回は第二種ベッセル関数を表す無限積分の式を、2つの不完全ガンマ関数で挟み、置き換えることによって、第二種ベッセル関数を精度保証付き数値計算する。
- ◎チェビシェフ級数を用いた非線形常微分方程式系の精度保証付き数値解法 / ○舩越 康太 (筑波大学), 高安 亮紀 (筑波大学) [概要]
本講演ではチェビシェフ級数を用いて非線形常微分方程式系の初期値問題の解を精度保証付きで得るための手法を紹介する.
具体的には,問題をある作用素方程式に書き換え,簡易ニュートン写像を定義し,この写像が縮小写像となることを示し,解の精度保証付き数値計算を実行する.
▷ 連続体力学の数理（１） ［3月4日：09:40-11:00：D］
- ◎Hyper Dual Numbersの行列表示を用いた微分計算手法の基礎理論整備 / ○井元 佑介 (東北大学), 山中 脩也 (明星大学), 浦本 武雄 (東北大学), 藤川 正毅 (琉球大学), 三目 直登 (東京大学) [概要]
Hyper Dual Numbers(HDN)は冪零性を持つ複数の元を用いて表される数で，実数空間の関数をTaylor級数展開に基づいてHDNの空間に拡張することで高階の微分の計算手法を構築することができる．本講演ではHDNの行列表示を定義することで，その行列表示を用いた任意階・多重階微分の計算手法を提案する．本計算手法は複合材料などに応用される材料構成則の高精度・高速な数値計算を実現することができる．
- ◎ 2次元Helmholtz方程式の1周期transmission問題に対するBurton-Millerの積分方程式を用いた高速直接解法 / ○松本 安弘 (京都大学), 西村 直志 (京都大学) [概要]
2次元Helmholtz方程式の1周期transmission問題における高速直接解法の先行研究として、multi-trace境界積分方程式を用いることで、Martinsson-Rokhlin型のアルゴリズムを破綻なく適用する方法が提案されているが、未知数の数が大きくなり数値計算時間が増大する問題がある。そこで本発表では、Burton-Millerの積分方程式を用いた高速直接解法を検討し、未知数の数の減少と数値計算時間の短縮を試みる。
- ◎遅延微分方程式の履歴方向に対するガレルキン法の誤差評価に向けて / ○杉谷 宜紀 (東北大学AIMR), 井元 佑介 (東北大学TFC), 宇田 智紀 (東北大学AIMR), 坂本 祥太 (東北大学理学研究科), 西口 純矢 (東北大学理学研究科) [概要]
遅延微分方程式は制御問題などで用いられ、微分が過去の状態に依存する特徴を持つ。その数値計算では従来のオイラー法などは時間の離散化と遅延の離散化が同一である為に特有の困難が生じる事がある。本講演では、時間方向と遅延方向を分離する偏微分方程式としての定式化に基づいて最近提唱されたガレルキン=クーンウィンダー法を紹介し、誤差評価などについて報告する。
- ◎解析解に基づく輻射輸送方程式の数値計算 / ○町田 学 (浜松医科大学) [概要]
輻射輸送方程式は積分項を持つ1階の微分方程式である。方程式は空間変数と時間変数に加えて角度変数をもち、数値計算は容易でない。解析解も限られた場合にしか知られていないが、本講演では近年得られた3次元での解析解を利用した数値手法を紹介する。球面調和関数で展開する点は古くから知られるPN法と同じであるが、3次元特異固有関数の間の直交関係を使って高速数値計算を実現する。
▷ 連続体力学の数理（２） ［3月4日：11:10-12:30：D］
- ◎位相流体解析とその計算手法開発の基礎理論について / ○横山 知郎 (京都教育大学数学科/JSTさきがけ) [概要]
曲面上の”一般的な”流れは理論的には数え上げを紹介する．さらに，穴あき円板上の非圧縮流のトポロジーと一対一対応する表現の具体的な構成できることを紹介する．特に，紹介する表現は計算機で実装するのに適したものであるばかりでなく，特異点や物理境界の生成や消滅を記述するのに適していることについても述べる．
- ◎位相的流体データ解析の応用：変換アルゴリズムと適用例 / ○宇田 智紀 (東北大学材料科学高等研究所) [概要]
2次元ハミルトン流れの流線位相構造を捉え文字化する理論が坂上・横山らによって提案され，その幅広い応用可能性への期待から計算機実現が急務となっている．本講演では，パーシステントホモロジーに基づいたレーブグラフの離散的定式化と，そこから導かれる流線トポロジーのツリー表現への変換アルゴリズムを紹介する．
- ◎射影有限要素法による Navier-Stokes 流れの計算における粘性係数依存性の改善 / ○内海 晋弥 (学習院大学) [概要]
射影有限要素法においては，Taylor-Hood 要素など，流速に圧力よりも1次高次の多項式を使った要素を用いられ，誤差評価が行われてきた．しかし，誤差解析に現れる定数は粘性係数に依存し，また，数値実験でもそれが観察されている．本報告では，流速と圧力に同じ次数の多項式を用いた場合に，粘性係数依存性が改善されることを見る．
- 一般J積分によるStokes問題における形状最最適化 / ○大塚 厚二 (広島国際学院大学), 中澤 嵩 (大阪大学) [概要]
形状最適化は、形状感度解析、最適化、数値計算方法を必要とする。 弾性においては、形状感度解析のための一般J積分、最適化のためのH1勾配法、数値計算法のための有限要素法を用いた体系的方法を構築している。Stokes問題では非圧縮性のため、弾性方程式のように一般積分を使用できなかったが、 Lagrangianの形状感度解析を行い、Stokes問題における一般積分を導出したので、使用例を示す。
▷ 連続体力学の数理（３） ［3月4日：13:30-14:50：D］
- ◎完全陽的な部分段階法による圧縮性熱対流の数値計算 / ○鳥生 大祐 (京都大学学術情報メディアセンター), 牛島 省 (京都大学学術情報メディアセンター) [概要]
本研究では，圧縮性熱対流に対する完全陽的な部分段階法を提案する．この手法では，圧力の空間変動成分に人工的な係数を乗じて音速を調整することで，基礎方程式の圧力項を陰的に扱う従来の半陰解法と同程度の時間刻み幅を設定し，連立一次方程式を解くことなく低マッハ数の圧縮性流れを高速に計算できる．提案手法はキャビティ内自然対流などに適用され，温度分布や壁面ヌセルト数の比較を通じてその妥当性を確認した．
- やわらかい固体における超音速すべり摩擦 / ○山口 哲生 (九州大学大学院工学研究院機械工学部門), 家敷 拓弥 (九州大学大学院工学府機械工学専攻) [概要]
物体同士がこすれあう現象であるすべり摩擦においては，多くの場合，すべり速度は物体の弾性波速度に比べて無視できるほど小さい．一方，ゴムやゲルなどやわらかい固体のすべり摩擦では，すべり速度が弾性波速度を上回る，”超音速”を容易に実現することができる．本研究では，まず摩擦実験を行い，超音速すべり速度条件下のゲルの変形や摩擦挙動について解析を行った．その結果，すべり速度がS波（横波）速度を上回るところで摩擦係数が急上昇することを見出した．また，接触問題における解析解や数値解を用いて現象の解析を行った．
- ◎長方形分割におけるあるHDG法の超収束について / ○及川 一誠 (早稲田大学) [概要]
Hybridizable Discontinuous Galerkin (HDG) 法はある特定の有限要素に対して超収束することが知られている．
最近では，超収束するための十分条件として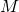
-decomposition理論が提案されている．
本講演では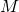，-decomposition理論を拡張した結果として，長方形分割において超収束する，ある特殊な有限要素が
得られたことを報告する．
- 混合型有限要素法による離散化 drift-diffusion 方程式の非線形ソルバー / ○鈴木 厚 (大阪大学 サイバーメディアセンター) [概要]
Drift-diffusion 方程式は半導体デバイスの数理モデルであり, 静電場と電子及び正孔密度分布を未知変数とする非線形システムで記述される. 電子及び正孔密度の勾配の値も未知変数として混合型の有限要素近似を適用する. 係数行列成分の静電場への指数関数的依存性は有限要素内での積分により取り扱い, 全体の非線形システムの Newton 反復を構成することができる. 従来, 非線形アルゴリズムとしてよく用いられる Gummel 反復法は電子及び正孔密度に不動点反復法, 静電場に Newton 反復を用いるものであるが, これを系全体の Newton 法の初期値の生成に利用することで効率的に求解できる.
▷ 数論アルゴリズムとその応用（１） ［3月4日：15:00-16:20：D］
- ◎同種写像暗号CSIDHの計算量評価と定時間実装の高速化 / ○小貫 啓史 (東京大学), 相川 勇輔 (北海道大学／東京大学), 山崎 努 (九州大学), 高木 剛 (東京大学) [概要]
耐量子暗号の候補の1つである同種写像暗号にCSIDHと呼ばれる方式がある. CSIDHは秘密鍵によって計算時間に大きな差が生じるが, 最近Meyerらによって定時間実装が提案された.
本発表では, CSIDHで必要とされる計算量を楕円曲線の定義体の演算回数で評価し, それに基づき, 高速化手法の定量的評価および安全性の評価を行う. さらに, Meyerらによる定時間実装の定量的な計算量評価も行い, その高速化についても考察を行う.
- ◎平面4次曲線の双接線に関する局所大域性 / 谷口 隆 (神戸大学理学研究科), 大下 達也 (愛媛大学理工学研究科), 内田 幸寛 (首都大学東京理学研究科), 伊藤 哲史 (京都大学理学研究科), ○石塚 裕大 (京都大学理学研究科) [概要]
平面4次曲線の双接線とは，2点で2重に接する直線のことをいう．双接線は複素数体上では28本あり，代数幾何において古くから研究されているが，その数論的な性質については分かっていないことも多い．この講演では，「双接線の存在条件が局所大域性を満たすか」という問題を考察し，一般には局所大域性を満たさないことを示す．すなわち，有理数体上の平面4次曲線であって，有理数体上は双接線を持たないが，実数体上およびすべてのp進体上で双接線を持つものが存在することを示す．また，そのような平面4次曲線を具体的に計算するアルゴリズムを紹介する．アルゴリズムの正当性の証明には，del Pezzo曲面の幾何と計算機によるSp(6,2)の部分群の計算を用いる．
- ◎Signatureを用いたGröbner基底を求めるアルゴリズムの効率的な簡約方法 / ○坂田 康亮 (横浜国立大学大学院環境情報学府) [概要]
2001年にFaugéreによりF5アルゴリズムが提案されて以降，signatureを用いたGröbner基底を求めるアルゴリズムに関して様々な手法や改良が提案されている．
この講演はsignatureを用いたGröbner基底を求めるアルゴリズムの効率化に関するもので，アルゴリズム内で主要な計算である簡約回数を削減する方法提案する．特に，簡約Gröbner基底を求める際に効果的な方法となっている．
- superspecial Howe 曲線の数え上げ / ○千田 駿人 (横浜国立大学環境情報学府) [概要]
超特別曲線とは，そのヤコビ多様体が種数個の超特異楕円曲線の直積と閉体上同型である代数曲線を指す．本講演では，超特別Howe曲線の数え上げに関するアルゴリズムを提案した．Howe曲線とは2つの楕円曲線で定義され，それらの射影直線上のファイバー積で表される．この曲線はEverett Howe氏によって研究なされており，超特別性に関するよい性質をもっている．これを基に超特別Howe曲線の数え上げに成功した．
▷ 数論アルゴリズムとその応用（２） ［3月4日：16:30-17:50：D］
- 円分体の相対類数の行列式公式の値の大きさの特異性とD-efficiencyについて / ○谷口 哲也 (金沢工業大学基礎教育部) [概要]
Demjanenko 行列は±1成分の行列で，この行列式の値は円分体の相対類数を表す．その値は±1をランダムに生成した行列式に比べて「極度に大きく」なることを数値実験にて観察している．数値的な観察結果の一例を挙げると， ±1をランダムに生成した行列式の値の分布の中においてDemjanenko行列式の値は平均から4.7標準偏差ほど大きな位置にあり，またHadamard行列がまだ見つかっていない716次行列に対応するDemjanenko行列式の値も極めて大きく，Hadamardの上限の約96.8%の大きさの桁数を実現している．
この「行列式の値が大きい」という性質は，例えば実験計画法などの実学の問題への応用につながる可能性があると講演者は考えている．
本講演ではDemjanenko行列について現状で持っている数値実験結果などについて報告したい．特にHadamardのboundとの比較，D-Optimal designs におけるD-efficiencyの漸近的挙動などについて述べたい．
▷ 数理ファイナンス（１） ［3月4日：09:40-11:00：E］
- 複合Hawkes型リスク過程モデルを用いた破産確率評価 / ○関根 順 (大阪大学大学院基礎工学研究科), 稲葉 麻友子 (大阪大学大学院基礎工学研究科) [概要]
保険金支払いの累積過程を複合Hawkes過程でモデル化したリスク過程を取り扱い、破産確率評価を行う。このリスク過程は、複合ポワソン過程を用いた古典的Cramer-Lundbergモデルや、レヴィ過程を用いたその一般化モデルとは異なり、独立増分性を持たないモデルであり、伝搬してゆくリスクのモデル化に適していると考えられる。複合Hawkes過程の持つアファイン過程としての性質を利用して、常微分方程式の解析を通した破産確率評価方法を提案する。
- ◎混合ポアソン過程の特性と破産理論への応用 / ○冨田 昌 (明治安田生命保険相互会社), 高岡 浩一郎 (一橋大学) [概要]
混合ポアソン過程において、各時点での条件付事故発生確率を事故発生のインターバルで時間積分したとき、当該ポアソン過程の強度パラメータの事前分布に依存せず常にパラメータ1の指数分布に従う事を示す。この性質を破産理論に応用し、事故発生過程と保険料設定について拡張されたルンドベリモデルは、一定の条件下で通常のルンドベリモデルと同一の破産確率を持つ事を示す。
- 株式，社債市場への投資を加味したexcess-of-loss再保険のロバスト最適化問題 / ○吉田 賢樹 (法政大学) [概要]
本研究は、モデルの曖昧性を回避しようとする保険者ためのexcess-of-loss再保険と株式、社債市場への投資の最適化問題である。この保険者の目的はモデルの曖昧性を仮定したとき満期での期待効用を最大化させるような戦略、つまり、株式、社債市場での最適な取引戦略、またexcess-of-loss再保険における最適な閾値を導くことである。最適戦略の導出には確率的動的計画アプローチを用いる。なお、効用関数は指数効用を考える。
▷ 数理ファイナンス（２） ［3月4日：11:10-12:30：E］
- ◎滑らかでないWiener汎関数に対する超関数微分とバリア・オプシ ョンのGreeks計算方法 / ○石谷 謙介 (首都大学東京) [概要]
自明でない定義関数を含むようなWiener汎関数は通常の意味での微分が存在しないことが知られているが、本講演ではこのような滑らかではないWiener 汎関数に対する超関数微分の計算方法を紹介する．さらに本提案手法を用いたバリア・オプションの1次オーダーのGreeks計算への応用例も紹介する．
- 金利変動を考慮した為替オプションの展開による近似評価 / ○永見 健次 (三菱UFJトラスト投資工学研究所(MTEC)) [概要]
為替デリバティブの精緻な評価を目指して、金利の変動を考慮した為替の確率ボラティリティモデルを考える。このモデルではオプション価格の厳密解は知られておらず、ここでは展開による近似評価法を提案する。さらに数値検証を行い、モンテカルロ・シミュレーションによる計算結果をベンチマークとして、本研究の近似評価法と特性関数の近似を用いた手法を比較する。
- Comparative Study on the Efficiency of Government expenditure in Agriculture / ○Wang Hongmeng (Graduate school of International Christian University), Kaneko Takuya (International Christian University) [概要]
In our presentation, we propose a hybrid type analyzing model by combining standard approaches for government’s effective resource allocation. In the past few decades, on one hand, quantitative analyses on the performance measurement using Data Envelopment Analysis (DEA) model and Stochastic Frontier Analysis (SFA) are prevalent and widely applied in many fields, especially in operations and management of enterprises. On the other hand, agricultural subsidies, which are controversial and pretty huge (more than one billion dollars a day) throughout many countries, urgently need to be evaluated scientifically and properly for sound government decision-making. Therefore, combining the DEA and SFA models together and utilizing mainly the OECD data of USA, EU, Japan and China, this paper takes a new perspective on the evaluation of agricultural subsidy efficiency and proposes different policy reform suggestions basing on the individualized analysis for each country or region. In general, we found that the results supported the hypothesis that the market distortion of agricultural subsidy should be as little as possible and subsidy strategies are different for each country due to the different agricultural development levels. Meanwhile, in the study, we also discovered the negative returns to scale phenomenon (called “NRS Trap”), which means the combined outputs decrease even when the combined input increase in some common cases. As a whole, using operations and management methods, this paper gives a new view on the evaluation of agricultural subsidy policies, makes policy assessment more specific and comprehensive, as well as provides a scientific reference for the government policy formulation.
- 日本のクレジット市場における信用サイクルの変動に関する分析 / ○廣中 純 (野村アセットマネジメント株式会社) [概要]
市場で観測可能な要因のほか, 市場で観測できない要因（frailty）を考慮した信用イベントの発生強度を表すモデルを提案する. また本モデルにより, 日本のクレジット市場における信用サイクルの変動要因の説明を試みる.
▷ 数理ファイナンス（３） ［3月4日：13:30-14:50：E］
- ◎離散時間モデルにおけるweak reflection principle / ○今村 悠里 (東京理科大学経営学部ビジネスエコノミクス学科) [概要]
Peter CarrとSergey Nadtochiyは１次元拡散過程に対して，バリアーオプションの静的ヘッジ公式を与えるペイオフ関数間の対応（Carr-Nadtochiy変換）を与えた．これはブラウン運動に対して成り立つことが良く知られている鏡像原理の一般化であると捉えられる．彼らの結果では１次元であることが本質的に働いているため，多次元拡散過程への一般化は難しいとみなされていたが，最近，d次元格子上のMarkov Chainについては同様の変換が存在することが分かった．本講演ではこの結果について報告する．
- 連続制御と確率インパルス制御の混合制御問題に対する数値計算アルゴリズムの提案(II) / ○内藤 瞭介 (法政大学理工学研究科), 安田 和弘 (法政大学) [概要]
第14回日本応用数理学会研究部会連合会で，連続制御と確率インパルス制御の混合制御問題に対する数値計算アルゴリズムの提案を行った．そのアルゴリズムは，Feng and Muthuraman (2010)で提案された，Policy Iteration Algorithmに基づく確率インパルス制御の数値計算アルゴリズムに連続制御を加えたものであった．連続制御を加えることで微分方程式に非線形項が現れることとなり，以前のアルゴリズムでは，その項を区分的に線形な関数で近似することで対応したが，本講演では，その非線形項にひとつ前のコスト関数を用いて対応するアルゴリズムを提案する．また，これらのアルゴリズムによる数値実験結果を与え，その比較を行う．
- 二項モデルにおけるDPを用いた期待効用とPFPPを用いた期待効用の比較 / ○佐藤 大地 (法政大学大学院理工学研究科), 安田 和弘 (法政大学) [概要]
日本応用数理学会2018年度年会において、Angoshtari, et al. [2018] で考えられているPredictable Forward Performance Processes（PFPP）とDynamic Programming（DP）の二項モデル下での期待効用の差に関する比較を乱数を発生させる形で数値実験を通じて行った。本講演では、市場の状況が当初の想定から変化させ、PFPPとDPの満期での期待効用の差にどのように影響するかを考察する。
- ポリアの壺から生成される二項モデルについて / 赤堀 次郎 (立命館大学), 仙葉 雄基 (立命館大学), ○琉 佳勳 (立命館大学) [概要]
株式市場のモデリングを考えるときに、良く知られたトイモデルとして、二項モデルがある。この二項モデルでは、利率と株価の上昇率、下落率が然るべき条件を満たしていれば、二項分布となるリスク中立確率が定まり、このリスク中立確率を使ってのオプションの価格付けが知られている。
この講演では、リスク中立確率がポリアの壺から決まる確率となる様な二項モデルを考え、この設定におけるオプションの価格付けについて議論する。
▷ 離散システム（１） ［3月4日：15:00-16:20：E］
- ◎計算量と乱数性から見た暗号の評価 / ○石井 夏海 (お茶の水女子大学大学院) [概要]
現在、国際標準として使用されている共通鍵暗号のうちの1つにAES-128があり、その鍵は大きな素数をパラメータとするDiffie-Hellman鍵交換で共有することが多い。攻撃者が交換の際のやり取りから鍵を入手できないように、鍵交換法は暗号と同等以上に安全でなければならない。そこで、将来AES-128の暗号化を鍵の全数探索法で破れる計算機が登場したとき、Diffie-Hellman鍵交換法の素数パラメータをどの程度大きくするべきか調査した結果を報告する。
- 高次元Rectilinear Steiner tree problemに対する分枝限定法の高速化の工夫 / ○宮本 裕一郎 (上智大学) [概要]
Rectilinear Steiner Tree Problem（RSTP）は典型的な組合せ最適化問題の1つでありNP-困難である．2次元RSTPに特化した高速な分枝限定法は数千ターミナルの問題例の最適解を1時間以内に求解可能であるが，3次元以上になると分枝限定法の速度は急激に落ちる．本講演では，3次元以上のRSTPに対する分枝限定法の高速化の工夫を提案し，数値計算実験による既存手法との比較を報告する．
- ◎周期的なAuxetic構造の生成手法 / ○石濱 和樹 (東京大学), 谷川 眞一 (東京大学) [概要]
Auxetic構造は負のポアソン比を有する構造であり，その特殊性からさまざまな応用が考えられている．本研究では,Auxetic構造の幾何的な特徴付けを利用し，Auxeticな周期的グラフ構造を列挙する手法を提案する．
- ◎Tree-based networkの構造定理と系統樹推定に関する諸問題への応用 / ○早水 桃子 (統計数理研究所，JSTさきがけ) [概要]
近年の系統学的データ解析では系統樹の拡張構造である「系統ネットワーク」が重要な役割を果たす．その中でもtree-based network (TBN)は理論生物学領域で特に注目されているが，計算量が解明されていない多くの基本的な問題があるため，統計学的応用には結びついていなかった．本講演では「TBNの構造定理」を与え，それがTBNに関する決定／探索，数え上げ，列挙，最適化などの諸問題を線形時間で（列挙は線形遅延時間で）解くアルゴリズムを統一的に導くことを示す．
▷ 離散システム（２） ［3月4日：16:30-17:51：E］
- ◎Improved Structural Methods for Nonlinear Differential-Algebraic Equations via Combinatorial Relaxation / ○大城 泰平 (東京大学) [概要]
微分代数方程式 (DAE) の数値計算では，初期値設定などの前処理が重要であり，組合せ最適化を用いた前処理手法が広く用いられる．この手法はある種の DAE には適用不能であり，そのような DAE は前処理可能な DAE に修正する必要があるが，既存の修正手法は主に線形DAEのみを対象とする．本発表では，非線形 DAE に適用可能な，陰関数定理と組合せ緩和に基づいた 2 種類の修正手法を提案し，数値計算結果を示す．
- 多重マトロイド制約最適化問題の近似アルゴリズムと整数性ギャップ / ○腰高 拓美 (東京大学大学院情報理工学系研究科数理情報学専攻) [概要]
線形関数最適化問題の制約条件として与えられるマトロイドが3つ以上の問題は、最適解の計算がNP困難である。本講演ではこの問題に対し自然に定義される線形計画緩和問題がもつ多面体の性質を用いて重みなしの場合に対する近似アルゴリズムを与えた。 さらに一部のマトロイドに対しては重みつきの場合にも同様の整数性ギャップが成り立つことを示した。
- 漸化式にもとづく多面体内の格子点の数え上げについて / ○平井 広志 (東京大学) [概要]
Zeilberger (1990) は，計算が難しい関数/数列に対し，それが満たす常微分方程式/常差分方程式を導いて解くことにより，値を計算する手法（ホロノミック法）を提案している．本発表では，その手法を多面体内の整数格子の数え上げ問題に応用することを試みる．
- No regret algorithms for online k-submodular maximization / ○相馬 輔 (東京大学) [概要]
オンラインk劣モジュラ最大化に対する多項式時間アルゴリズムを与える．提案するアルゴリズムは，劣線形の近似リグレット(no approximate-regret)を達成し，オフライン最大化に対する既存の近似アルゴリズムをオンライン最適化へ拡張したものと見なせる．提案アルゴリズムは，Blackwellの定理とオンライン線形最適化を組合せたもので，オンライン非単調劣モジュラ最大化の既存研究と比べてよりシンプルで簡潔な解析を与える．
▷ 数理医学 ［3月5日：11:10-12:30：A］
- NF-κBシグナル伝達経路における振動現象を制御する機構とそのパラメータの解析 / ○畑中 尚也 (大阪大学大学院基礎工学研究科), 関 崇生 (国立研究開発法人理化学研究所), 井上 純一郎 (東京大学医科学研究所), 鈴木 貴 (大阪大学数理・データ科学教育研究センター) [概要]
NF-κBは数百もの生体機能を制御するタンパク質であり，刺激の種類によって異なる活性化機構；古典的経路，非古典的経路を持つ．NF-κBが正常に機能するためには，適切な周期で細胞質-核間を行き来することが必要である．古典的経路ではほぼすべての細胞でNF-κBの細胞質-核間の振動が得られるのに対して，非古典的経路では細胞によって挙動が異なる．本講演ではこのような振動現象を引き起こす機構と，細胞ごとに挙動が異なる原因となるパラメータについて報告する．
- ◎数理解析を活用したSAPKシグナル時空間制御機構の解明 / ○森泉 寿士 (東京大学医科学研究所 分子シグナル制御分野), 中村 貴紀 (東京大学医科学研究所 分子シグナル制御分野), 曺 永旻 (大阪大学大学院 基礎工学研究科 システム創成専攻 数理科学領域), 鈴木 貴 (大阪大学 数理・データ科学教育研究センター), 武川 睦寛 (東京大学医科学研究所 分子シグナル制御分野) [概要]
外界からの様々な刺激を細胞内へ伝達して適切な細胞応答を誘導する重要なシグナル伝達システムの1つにSAPK経路がある。SAPK経路は、SAPKKK-SAPKK-SAPKの順にリン酸化されることにより活性化し、細胞死、炎症などの細胞応答に中心的な役割を果たす。SAPK経路構成因子の中でSAPKKは経路を仲介するリン酸化酵素としての機能以外に殆どわかっていない。今回我々は、数理解析を用いてSAPKKの時空間的挙動から新たなSAPK経路制御機構を見出したので報告したい。
- 実空間や情報空間の『形』を観る方法の開発 / ○中村 直俊 (大阪大学・数理・データ科学教育研究センター) [概要]
多様性を示す様々なサンプル間の差異の程度とその支配要因を調べることは、生命科学や医学にとって重要な課題である。私たちは、サンプルを実空間または情報空間の中の「形」としてとらえ、形の差を定量化することによってサンプル間の多様性を可視化する方法を開発している。本発表では、この手法の適用可能性を議論する。
▷ 科学技術計算と数値解析（１） ［3月5日：13:30-14:50：A］
- ◎入出力関係式を用いた少ないデータからのアトラクタの再構成 / ○小松 瑞果 (神戸大学大学院システム情報学研究科) [概要]
入出力関係式は，主にシステムズバイオロジーの分野において構造的同定可能性解析に用いられる，モデルの入力と出力，及び，パラメータの関係を表す式である．本発表では，入出力関係式の応用として，アトラクタの再構成手法について述べる．
- ◎On the Chaotic Dynamics in Homothermal Maintenance of Skunk cabbage / ○エルデネバートル トゥルトグトフ (岩手大学総合科学研究科), 川崎 秀二 (岩手大学総合科学研究科) [概要]
The plant called Skunk Cabbage is known to have a remarkable feature that it has a heating organ and retains its body temperature almost constant around 22~23 [°C] at the end of winter.
As the mechanism of the homothermal maintenance, we have found that the control has linear equilibrium phase and nonlinear nonequilibrium phase. We consider, from a data analytic study, how well the Duffing equation model fit to the latter phase.
- 双曲型平衡点近傍の局所Lyapunov関数を用いたホモクリニック軌道の精度保証 / ○新田 光輝 (電気通信大学), 山本 野人 (電気通信大学) [概要]
双曲型平衡点を持つ連続力学系に対し、その平衡点近傍における局所Lyapunov関数を精度保証付き数値計算を用いて構成する方法が提案されている。本講演では局所Lyapunov関数の応用例として、ホモクリニック軌道の存在検証を行う精度保証法を提案する。局所Lyapunov関数が検証手順のどこで利用されているかに重点を置いて説明する予定である。
- 非双曲型平衡点近傍における局所Lyapunov関数の精度保証による構成 / ○寺坂 元 (電気通信大学情報理工学研究科), 中村 正男 (電気通信大学情報理工学研究科), 山本 野人 (電気通信大学情報理工学研究科) [概要]
精度保証による局所的なLyapunov関数の構成は力学系の解析のための非常に強力な道具であることがわかってきた．しかし，これらはこれまで双曲型平衡点近傍でのみ構成可能であった．この講演では，非双曲型平衡点近傍のうち，標準形定理を上手く利用できる場合において局所Lyapunov関数の構成・検証方法を報告する．
▷ 科学技術計算と数値解析（２） ［3月5日：15:00-16:20：A］
- ◎ Hypercircle法による有限要素解の局所事後誤差評価について / ○中野 泰河 (新潟大学大学院 自然科学研究科), 劉 雪峰 (新潟大学大学院 自然科学研究科) [概要]
本研究ではPoisson方程式に対して，Hypercircle法による有限要素解の事後局所誤差評価を提案する。
提案手法によって、解の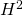
正則性によらずに関心のある領域における有限要素解の局所誤差評価を得ることができる．
本講演ではL字形領域上のPoisson方程式に対する数値実験の結果も紹介する．
- 気候変動下の捕食者-被食者生態系の数理モデル構築とシミュレーション / ○坂田 克己 (公立・前橋工科大学) [概要]
気候変動下の捕食者-被食者生態系について、捕食者と被食者のバイオマス間の相互情報量、シャノンエントロピーの削減量で測ったシステムの調整能を導入した数理モデルを構築した。生態学の分野でよく研究されている、閉鎖湖沼におけるザリガニ、バス生態系(Drury and Lodge 2009)についてシミュレーションを実施し、前述の数理モデルについて考察する。
- ◎散逸型微分方程式の構造保存モデル縮減 / ○稲場 俊弥 (東京大学), 松尾 宇泰 (東京大学) [概要]
大規模な力学系を解く際，モデル縮減を用いて次元を落とすことで高速に解くことができる．特に近年では，元の問題が有する構造を保存することで安定に縮減を行う手法が，特定の系に対し考察されてきた．本発表では，散逸型の微分方程式において，汎用的な構造保存モデル縮減の手法の一つを提案し，数値的に解きづらいCahn–Hilliard方程式を用いた数値実験結果について述べる．
- 高次非線形性を持つ微分方程式に対する安定な陰的線形スキームの構築 / ○髙橋 俊太 (東京大学計数工学科数理3研), 松尾 宇泰 (東京大学計数工学科数理3研) [概要]
微分方程式に対する構造保存解法はその有効性が広く知られているが、一般に非線形な問題に対するスキームは非線形となり計算量が大きくなる。
それを緩和する陰的線形化手法も知られているが、安定性の確保が限定的であった。
本講演では、安定性を担保するより一般的な枠組を提案し、実際にある種の常微分方程式に対する数値解によりその正当性を確認する。
▷ 科学技術計算と数値解析（３） ［3月5日：16:30-17:50：A］
- 佐藤超函数のFourier変換の数値計算法 / ○緒方 秀教 (電気通信大学大学院情報理工学研究科情報・ネットワーク工学専攻) [概要]
本講演では、佐藤超函数論に基づくFourier変換の数値計算法、および、その佐藤超函数のFourier変換への拡張について述べる。佐藤超函数論とは複素関数論に基づく一般化関数の理論である。この理論においては、Fourier変換はFourier-Laplace変換によって得られる複素解析関数の解析接続によって得られ、これを数値的に計算すれば従来の方法に比べて効率的にFourier変換が計算できる。また、古典的な積分としては収束しないような佐藤超函数のFourier変換も、佐藤超函数論の考え方を用いて数値計算できることも示す。
- ◎等角写像による二重指数関数型数値積分公式の改良 / ○京谷 駿希 (東京大学), 田中 健一郎 (東京大学) [概要]
二重指数関数型数値積分公式(DE公式)は, 変数変換を用いた高精度な数値積分法である. ところが, 被積分関数が積分経路の近くに特異点をもつ場合, それらによる悪影響を受けやすいという弱点があり, 特異点に着目した等角写像によってこれを改良する試みがSlevinsky, Olver(2015)によって行われた. 本発表ではSlevinsky, Olverの発想を用いつつ, 新たにDE公式の一般化と見ることができる変数変換を構成し, より強力にDE公式を改良する方法を提案する.
- ◎再生核ヒルベルト空間に属する関数に対する点交換による求積公式の設計 / ○大城 隆之介 (東京大学), 田中 健一郎 (東京大学) [概要]
高次元空間上の関数の数値積分は一般的に難しいことが知られている．高次元空間上の関数の数値積分に対するアプローチの一つとして再生核ヒルベルト空間上の積分作用素を近似する手法がある．この積分作用素を近似する手法において，数値積分を行うときに関数を評価する点をどのように選ぶかはその近似精度に大きく影響する．しかし，このときの点配置をどのようにとればよいのかは難しい問題であることが知られている．本発表では再生核ヒルベルト空間に含まれる関数に対し，その積分作用素を近似する点を交換していくことにより改善を目指す手法について説明する．
▷ CAEモデリングとデータ活用 ［3月5日：11:10-12:30：B］
- 金属積層造形向けサポート設計技術の開発 / ○濱口 崇志 (（株）日立製作所 機械イノベーションセンタ), ヤン インジャ (（株）日立製作所 材料イノベーションセンタ), 朴 ミンソク (（株）日立製作所 材料イノベーションセンタ) [概要]
金属積層造形では，熱収縮による変形を抑制するために，支持構造であるサポートの設計が重要である．
従来，サポート設計は，試作と評価を繰り返しており，長時間を要していた．
そこで，本研究では，造形プロセスシミュレーションを用いたサポート設計技術を開発し，
レーザ条件とサポート制約を入力することで，短時間で推奨するサポート配置を提案可能とした．
- 重合メッシュ法に対応した任意形状３次元表面き裂メッシュ生成 / ○和田 義孝 (近畿大学) [概要]
重合メッシュ法は２つの独立したメッシュを重ね合わせて１つの有限要素モデルとして解析できる特徴がある。このためマルチスケールやき裂のモデル化が容易である特徴がある。しかし、メッシュ生成の労力が全くなくなるわけではない。著者らはこれまでも重合メッシュ法のためのメッシュ生成手法の開発に取り組んできたが多くの制約があった。そこで本研究では複数の表面き裂モデル生成を目的とした手法を提案する。
- ◎XFEMを活用したCFD・FSI計算 / ○澤田 有弘 (産業技術総合研究所) [概要]
本講演では、FEMを不連続関数の近似も取り扱えるように拡張したXEFMを、空間二次収束を示す一種のカットセル型FEMとして、物体周りの流れの計算に適用した研究を紹介する。XEFMは、メッシュはあるがメッシュは意識しない計算手法の一種であり、境界適合メッシュ法では取り扱うことが困難であるような連成計算を可能としたり、流体のみの計算を飛躍的に容易なものとしたり、多くの利点と将来性を有することを示す。
- ◎大領域変動問題の界面追跡におけるメッシュ制御 / ○山田 知典 (東京大学) [概要]
界面追跡法による流体構造連成（Fluid-Structure Interaction, FSI）解析においては，構造側の剛体運動あるいは大変形等に伴って流体領域にメッシュのゆがみが発生し，これに起因したFSI解析の破綻が大きな問題となっている．本研究ではFSI解析の安定性向上のため，合理的なメッシュ制御技術の開発に向けた検討を行う．
▷ 折紙工学（１） ［3月5日：13:30-14:50：B］
- ◎エネルギ吸収量向上のための折畳構造の圧潰特性の研究 / ○伊藤 大悟 (明治大学), 石田 祥子 (明治大学) [概要]
薄肉の円筒構造の圧潰特性に関する研究の中で,インバーションという優れたエネルギ吸収特性をもつ座屈があることが知られている.本研究の目的は,折畳構造によってこの変形を安定に生じさせることのできる構造を設計し,性能を評価することである.設計変数が異なる構造を設計し,静的な圧縮試験を行った結果を報告する.
- 折紙構造を採用する超長部材のエネルギー吸収性能の検討 / ○陳 暁詩 (明治大学), 楊 陽 (明治大学), 趙 希禄 (埼玉工業大学), 萩原 一郎 (明治大学) [概要]
一般に真直材を圧潰するのは困難で初期のピーク荷重は高く綺麗に規則正しく圧潰させるのは困難なことから
自長の7割程度しか潰れない欠点がある。そこで反転螺旋構造を利用することによりこれらの欠点が解消される
ことは既に報告されている。しかい、その確認は1m以下の長さのものに対してであった。ここでは四角形及び六角形断面で3mと超長
部材で検討を試みる。
- ◎折り畳み構造内流れの特性評価 / ○水谷 建太 (明治大学), 中 吉嗣 (明治大学), 石田 祥子 (明治大学) [概要]
流体の輸送には血管やパイプのように円筒形状が用いられることが多い。本研究ではより効率的な流体輸送のために、折り畳み構造を用いた流れの評価を目的とする。折り畳み構造は筒の壁面に規則的な折線が施されており、展開収縮の過程で筒内部の形状が変化する。そこで従来の単純な円筒内流れとの違いをCFDによるシミュレーションを用いて明らかにし、折り畳み構造の流体力学的特性を調査した結果を報告する。
▷ 折紙工学（２） ［3月5日：15:00-16:20：B］
- Origami Simulator を用いた曲線折りのシミュレーション / ○三谷 純 (筑波大学), 佐々木 好祐 (筑波大学), 野川 成己 (筑波大学) [概要]
GhassaeiらによるOrigami Simulatorを用いることで、展開図を折り線に沿って折る過程をシミュレートすることができる。折り線は直線であることが前提とされるが、短い線分の集合によって曲線を近似することで、曲線折りをシミュレートすることもできる。ただし、その際には、可展面のrulingに相当する補助線を適切に入力することが重要である。本発表では、このを補助線の配置を適切に行う事を目指した、異なる2つのアプローチについて発表する。
- ビーズ正二十面体上の閉測地線 / ○山岸 義和 (龍谷大学), 野田頭 美羽 (龍谷大学), 中島 香歩 (龍谷大学) [概要]
ビーズ編みによって、グラフと絡み目と折り紙の自然な対応を考える。ビーズ正二十面体の族は、2つの自然数の組 (p,q) で添字付けされる。m を自然数とし、p,q を互いに素な自然数とするとき、(mp,mq) 型のビーズ正二十面体上の測地線は、連続な正二十面体上の (p,q)型の閉測地線に自然に対応する。
- ◎円内接八角形の外接円半径公式の計算結果について / ○森継 修一 (筑波大学図書館情報メディア系) [概要]
円内接多角形の各辺長が与えられたとき、多角形の面積、外接円の半径、およびそれらの関係を表す多項式を求めることは、幾何学における古典的問題である。三角形に対するHeronの公式、円内接四角形に対するBrahmaguptaの公式は古くから知られていたが、五角形以上に対しては、Robbins(1994)が面積公式を求めるまで、長らく未解決のままだった。2011年、筆者は円内接七角形の外接円半径公式を求めることに世界で初めて成功したが、今回、それを八角形の場合まで拡張した。七角形の場合と八角形の場合は統一した公式で表現されるため、これによりひとつの問題が完結したことになった。
- ◎折り畳み可能な半割円筒の半径方向強度に関する研究 / ○五味 正輝 (京都大学工学研究科 航空宇宙工学専攻), 杉山 文子 (京都大学工学研究科 航空宇宙工学専攻) [概要]
本研究では，折紙工学によって提案された円筒折りとして知られる折り畳み方を用いた半割円筒状構造を，シェルターや仮設住宅等に応用することを想定し，その折り畳み特性及び半径方向強度について，有限要素法を用いて評価を行った．周期的なジグザグ面で構成されるこの構造は，折紙パターンを持たない通常の円筒に比べて，半径方向の強度，剛性とも非常に高く，また特に反転螺旋型円筒折りに関しては折り畳み特性にも優れている
▷ 折紙工学（３） ［3月5日：16:30-17:50：B］
- 折紙式輸送箱の振動遮断について / ○阿部 綾 (明治大学), 寺田 耕輔 (奈良高専), 萩原 一郎 (明治大学) [概要]
折紙工学研究の一環として、緩衝材としての役割と運搬箱の両方の役割を持たせる折紙式輸送箱が開発された。運搬対象物はそれぞれに極力避けたい周波数帯域があるため、問題となる周波数帯域で伝達特性を低くする方法を、外箱について最適化することで、これまでに検討してきたが、さらに外箱を2重箱にすることによる検討を行い、考察する。
- 折紙ロボット用２次元展開図の検討 / ○楊 陽 (明治大学), ルイス ディアゴ (明治大学), 萩原 一郎 (明治大学) [概要]
ロバートラングのTreeMakerに始まり多くの折紙設計ソフトがあるが、これらは人間を対象としたものである。これをロボットで折らす試みは多く見られるが、いずれも機構やセンサーなど複雑なものとなり袋小路に入った感がある。ここでは折紙ロボっトとしては折り曲げと糊付け、展開の機能だけ付与し、展開図を工夫するという真逆のアプローチをとる、ここではその一例を述べる。
- ◎折り畳み構造を利用した防振機構における空気ばねの応用 / ○稲本 知也 (明治大学), 石田 祥子 (明治大学) [概要]
Kresling patternからなる円筒型折り畳み構造は双安定性を有し，この構造に線形ばねを付加した防振機構が開発されている。本研究では新たに円筒折り畳み構造の内部に空気を密閉させ、線形ばねではなく空気ばねを作り出し代用することで折り畳み構造をそのまま用いることのできる防振機構を提案、その力学的特性を検証した。本講演では本防振機構の特性及びその優位性を報告する。
▷ 計算の品質（３） ［3月5日：11:10-12:30：C］
- 再現性のある区間行列積の計算法 / ○尾崎 克久 (芝浦工業大学) [概要]
計算機環境に依存せずにビット単位で完全一致する数値計算結果を得る再現性について，近年活発にアルゴリズムや実装の研究が進められている．本研究では，いくつかの仮定のもとで再現性のない従来の高速なBLASの関数を用いて区間行列積を計算する方法を紹介し，計算コストと得られる区間幅に関する数値実験結果を紹介する．
- ◎悪条件行列に対するCholeskyQRアルゴリズムとその比較 / ○寺尾 剛史 (芝浦工業大学), 尾崎 克久 (芝浦工業大学), 荻田 武史 (東京女子大学) [概要]
本発表では、列フルランク行列に対するthin QR分解の数値計算法について述べる。CholeskyQR2アルゴリズムは、CholeskyQRアルゴリズムで計算可能な行列に対して、直交性を改善する高速な計算手法である。我々は、CholeskyQRアルゴリズムで計算が困難な悪条件行列に対しての前処理法を複数提案する。また、数値実験により悪条件行列に対する提案手法の安定性および直交性や残差、計算速度に関する提案手法の有効性を示す。
- 浮動小数点演算に関する符号付き相対誤差について / ○小林 亮太 (芝浦工業大学), 尾崎 克久 (芝浦工業大学) [概要]
Jeannerod氏とRump氏によって，指数部の制約が無いことを条件とした浮動小数点演算に対する相対誤差の最適な評価が示された．本研究では，先行研究を基に議論を拡張し，浮動小数点演算（和・差・積）に対する符号付き相対誤差の最適な評価を示す．また，積におけるアンダーフロー発生時や除算についての考察も併せて紹介する．
▷ 数理設計（～15:10） ［3月5日：13:30-15:10：C］
- A new energy-gap cost functional approach for the exterior Bernoulli free boundary problem / ○Rabago Julius Fergy (Department of Complex Systems Science, Graduate School of Informatics, Nagoya University), Azegami Hideyuki (Department of Complex Systems Science, Graduate School of Informatics, Nagoya University) [概要]
The solution to a free boundary problem of Bernoulli type, also known as Alt-Caferelli problem, is studied via shape optimization techniques. In particular, a novel energy- gap cost functional approach with a state constraint consisting of a Robin condition is proposed as a shape optimization reformulation of the problem. Accordingly, the shape derivative of the cost is explicitly determined, and using the gradient information, a Lagrangian-like method is used to formulate an efficient boundary variation algorithm to numerically solve the minimization problem. The second order shape derivative of the cost is also computed, and it is shown how the Hessian information can be utilized to formulate a second-order optimization procedure based on a Newton-type method for resolving shape optimization problems. The feasibility of the newly proposed method and its comparison with the classical energy-gap type cost functional approach is then presented through various numerical results.
- 最適密度分布と安定なスキーム / ○海津 聰 [概要]
全質量に制約 c_1がある各質量分布 xは体積力と応力の下により仕事量 j_0(x)が定まる. 最小仕事量 min j_0(x)を与える密度分布 x^*が最適密度である.
本報告は最適密度分布 , x^*の存在を与える条件の下で, x^*を数値的に求める安定なスキームを提案するものである.
- 計算機援用証明によるラプラス作用素の固有値の最小化問題を考える / ○劉 雪峰 (新潟大学) [概要]
数理設計などの分野では、多くの問題が微分作用素の固有値問題の最小化問題に帰着する。本研究では、三角形領域に定義されるラプラス作用素の固有値問題について、三角形の直径が固定されるときの固有値の最小化問題を考える。特に、最小化問題に関わる微分作用素の固有値の摂動への検討には、微分作用素の固有値と固有ベクトルの厳密計算と評価が重要な役割を果たしている。
- ◎スポーツシューズの変形特性に関する評価指標と形状最適化 / ○野々川 舞 (アシックス), 竹内 謙善 (TXデザイン), 畔上 秀幸 (名古屋大学) [概要]
スポーツシューズは走行中の衝撃を緩和する緩衝性と正しい姿勢を保つ安定性を評価指標として設計される．本講演では，2つの指標に対して2つの境界条件を用意して，それらに対するソール（超弾性体を仮定）の変形から2つの近似変形平面を定義する．それらの近似変形平面のパラメータを用いて緩衝性と安定性の評価関数を定義し，形状最適化問題を定式化する．さらに，数値例でこの方法の有効性を確認する．
- 形状最適化問題における評価関数の2 階微分について / ○畔上 秀幸 (名古屋大学) [概要]
偏微分方程式の境界値問題が定義された領域の境界形状を最適化する問題（形状最適化問題）において，領域変動に対する評価関数の2階微分（2階形状微分）を評価する２つの方法を示し，それらを用いた形状最適化問題の解法（H1 Newton 法）を２つ提案する．また，数値例によってそれらの性能について考察する．
▷ 産業における応用数理（１） ［3月5日：13:30-14:50：D］
- データコラボレーションによる分散データ協調解析 / ○櫻井 鉄也 (筑波大学), 今倉 暁 (筑波大学), 二村 保徳 (筑波大学), 叶 秀彩 (筑波大学), アランニャ クラウス (筑波大学), ボグダノバ アンナ (筑波大学) [概要]
本講演では、各機関・組織が保有する分散したデータを一カ所に集約させることなく効果的にデータ解析を行う技術について述べる。これにより、データサイズの巨大化や秘匿情報保護、規格が異なるなどデータを統合して解析することが困難な状況において、元データを共有することなく解析を行う。
- ◎待ち行列を用いた宅配ボックスサービスのモデル化と解析 / ○日出山 慎人 (筑波大学システム情報工学研究科), Phung-Duc Tuan (筑波大学システム情報系), 岡田 幸彦 (筑波大学システム情報系) [概要]
サービスシステムの動的変化を解析する方法の1つとして，待ち行列理論が知られている．本講演では，宅配ボックスサービスを含む宅配サービスシステムを待ち行列モデル化し，準出生死滅過程として解析する．また，講演中で定義された各性能評価指標について解析結果とシミュレーション結果を同時に確認し，考察を行う．
- 最小二乗最小ノルム解の右前処理を用いた制約と半導体製造プロセスへの適用 / ○木村 泰己 (東芝メモリ), 松縄 哲明 (東芝メモリ), 三本木 省次 (東芝メモリ) [概要]
特異値分解による打ち切り最小二乗最小ノルム解において、係数行列に前処理を施す事により、最大特異値のみで打ち切った解を任意の関数に制約する手法を提案する。
先験情報として解の概形が分かっている時、本手法を適用すれば必要な特異対の数が少なくなるためRandomized SVDを用いた特異値分解の高速化が可能となる。
本手法が半導体リソグラフィーモデルの解法に有効であった事を報告する。
- 半導体製造プロセスにおける応力予測問題の解法 / ○松縄 哲明 (東芝メモリ), 木村 泰己 (東芝メモリ), 乙幡 幸雄 (東芝メモリ), 三本木 省次 (東芝メモリ) [概要]
半導体製造に用いるマスクプロセスでは、透明基盤上に堆積させた遮光性膜をエッチングすることで設計回路パターンを形成する。エッチングにより膜応力が変動するため、パターンの位置ずれが起こる。この位置ずれを精度良く予測し、補正する必要があるが、従来法の多項式を用いた簡易モデルでは精度不足が課題となっている。本発表では、この応力予測問題を、従来よりも変数を増やした線形方程式に定式化し、計測データのノイズの影響を低減するために特異値分解による打ち切り最小二乗法を用いることで高精度化が可能であることを報告する。
▷ 産業における応用数理（２） ［3月5日：15:00-16:20：D］
- 一細胞RNAシーケンス法に基づく細胞集団構造の発見 / ○尾崎 遼 (筑波大学 医学医療系/人工知能科学センター) [概要]
一細胞RNAシーケンス法により、数百から数万細胞の遺伝子発現量計測データが得られるようになった。しかし、これまでのRNAシーケンス法と異なり、個々の細胞は様々な階層での生物学的不均一性を持つため、遺伝子発現量変動の解析を行うには、細胞集団構造を教師なし学習で推定する必要がある。そこで、拡散マップ法を用いることで、細胞集団内の潜在的構造を推定し、遺伝子発現変動解析からその妥当性を検討した。
- 高次元のシミュレーションベース連続最適化に対する確率的探索アルゴリズム / ○秋本 洋平 (筑波大学) [概要]
産業におけるパラメータ最適化では，最適化対象となるパラメータを入力としたシミュレーションを通してのみ目的関数値が求まる状況がしばしば見受けられる．このようなシミュレーションベース最適化に対して，進化計算などの探索法は有効とされているが，その多くは高々100個程度の変数の最適化を想定している．本講演では，トポロジー最適化などに現れるような高次元最適化問題に対する，時間的および空間的計算量を考慮した確率的探索アルゴリズムについて述べる．
- ◎複素モーメント型部分空間を用いた教師あり次元削減法の提案 / ○今倉 暁 (筑波大学), 松田 萌望 (筑波大学), 叶 秀彩 (筑波大学), 櫻井 鉄也 (筑波大学) [概要]
本講演では，高次元特徴量を持つデータに対する次元削減法として，複素モーメント型部分空間を用いた新しい教師あり手法を提案する．従来の行列トレースの最大化・最小化に基づく次元削減法が少数の固有ベクトルのみを用い次元削減するのに対し，提案法は複数固有ベクトルを含む複素モーメント型部分空間を用いることで，分類性能の改善を図る．
▷ ウェーブレット（１） ［3月5日：13:30-14:50：E］
- Fractional Ridgelet Transformについて / ○藤井 克哉 (筑波大学), 木下 保 (筑波大学) [概要]
リッジレット変換とは，ラドン変換の像を1次元ウェーブレット変換する変換である．本講演では，デルタ関数がある近似式によって表現されることに着目してFractional リッジレット変換を提案し，逆変換やその変換の持つ様々な性質を探る．
- On Parseval Frames for Multidirectional Expansions and a Discretization Scheme of the Inversion of the Radon Transform / ○木下 保 (筑波大学), 藤ノ木 健介 (東海大学) [概要]
多方向へ展開をするためのパーセバルフレームとラドン変換の再生公式の離散化について、201７年秋の応用数理学会で報告した。多方向の度合いはパラメータの大きさによってより詳細にコントロールできるが、その数値実験や検証を具体的な関数を用いて行った結果を今回報告する。
▷ ウェーブレット（２） ［3月5日：15:00-16:20：E］
- 複素連続ウェーブレット解析と離散定常ウェーブレット解析の聴性定常反応比較 / ○井川 信子 (流通経済大学), 守本 晃 (大阪教育大学), 芦野 隆一 (大阪教育大学) [概要]
自作の聴性誘発脳波計測機器を用い，SAM音刺激を与えて得られたヒトの聴性誘発脳波データに対して複素連続ウェーブレット解析および離散定常ウェーブレット解析をそれぞれ実施した。その結果を比較してその解析妥当性を考察する。
- 任意実数ダイレーション正規直交ウェーブレット基底の応用 / ○戸田 浩 (豊橋技術科学大学), 章 忠 (豊橋技術科学大学) [概要]
任意実数ダイレーション正規直交ウェーブレット基底を用いた，Hilbert変換ペアのウェーブレット・フレームの構成法と，それを基礎にした連続ウェーブレット係数の定義，信号解析，および信号処理について発表します．
- 四元数窓フーリエ変換に関係する不確定性原理 / ○芦野 隆一 (大阪教育大学) [概要]
四元数窓フーリエ変換に関係する不確定性原理は既に知られているが，ここでは四元数フーリエ変換に関する不確定性原理を基にした証明を紹介する．